JEE 2015 :: Advanced 2015 :: Physics 2015

• Advanced 2015 - Physics 2015
• Advanced 2015 - Chemistry 2015
• Advanced 2015 - Mathematics 2015

Consider a concave mirror and a  convex lens  ( refractive index=1.5) of focal length 10 cm each, separated by a distance of 50cm in air (refractive index=1) as shown in the figure. An object is placed at a distance of 15 cm from the mirror. Its erect image formed by this combination has magnification M₁. When the set up is kept in a medium of refractive index. $\frac{7}{6}$, the magnification becomes M₂. The magnitude   $\mid\frac{M_{2}}{M_{1}}\mid$   is

Answer:

Explanation:

Case I

   Reflection from mirror

  $\frac{1}{f}=\frac{1}{v}+\frac{1}{u}\Rightarrow\frac{1}{-10}=\frac{1}{v}+\frac{1}{-15}$

  $\Rightarrow$          v=-30

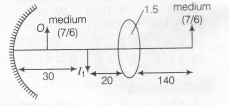
For lens              $\frac{1}{f}=\frac{1}{v}-\frac{1}{u}$

                         $\frac{1}{10}=\frac{1}{v}-\frac{1}{-20}$

                                      v=20

     $|M_{1}|=|\frac{v_{1}}{u_{1}}||\frac{v_{2}}{u_{2}}|$

           $=\left(\frac{30}{15}\right)\left(\frac{20}{20}\right)$

    =  2 X 1=2        (in air)

Case  II For mirror , there is no change

 v=-30

For lens

$\frac{1}{f_{air}}=\left(\frac{3/2}{1}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$

      $\frac{1}{f_{medium}}=\left(\frac{3/2}{7/6}-1\right)\left(\frac{1}{R_{1}}-\frac{1}{R_{2}}\right)$

 with            f_{air  =10cm}

 We get    $\frac{1}{f_{medium}}=\frac{4}{70}cm^{-1}$

              $\frac{1}{v}-\frac{1}{-20}=\frac{4}{70}$

$\frac{1}{v}+\frac{1}{20}=\left(\frac{2}{7}\right)\left(\frac{2}{10}\right)=\frac{4}{70}$

    $\frac{1}{v}=\frac{4}{70}-\frac{1}{20}$

    v=140,

     $|M_{2}|=|\frac{v_{1}}{u_{1}}||\frac{v_{2}}{u_{2}}|$

                             $=\left(\frac{30}{15}\right)\left(\frac{140}{20}\right)$

                           $=2\left(\frac{140}{20}\right)=14$

                        $\Rightarrow$      $|\frac{M_{2}}{M_{1}}|=\frac{14}{2}=7$

A Young's double slit interference  arrangement with slits S₁   and S₂ is immersed in water (refractive index=4/3)  as shown in the figure. The positions pf maxima on the surface of water are given by   $x^{2}=p^{2}m^{2}\lambda^{2}-d^{2}$ , where  $\lambda$    is the wavelength  of light in air (refractive index=1)  , 2d is the seperation between the slits and m is an integer . The value of p is 

Answer:

Explanation:

$\mu(S_{2}P)-S_{1}P=m\lambda$

$\Rightarrow$                $\mu\sqrt{d^{2}+x^{2}}-\sqrt{d^{2}+x^{2}}=m\lambda$

$\Rightarrow$              $(\mu-1)\sqrt{d^{2}+x^{2}}=m\lambda$

$\Rightarrow$             $(\frac{4}{3}-1)\sqrt{d^{2}+x^{2}}=m\lambda$

   or                      $\sqrt{d^{2}+x^{2}}=3m\lambda$

 Squaring this equation we get,

                $x^{2}=9m^{2}\lambda^{2}-d^{2}$

$\Rightarrow$       $P^{2}=9$          OR  P=3

• Advanced 2015 - Physics 2015
• Advanced 2015 - Chemistry 2015
• Advanced 2015 - Mathematics 2015